In this post you will learn how to graph sine and cosine functions with ease. You will understand how amplitude, period, phase shift, and vertical shift affect the graph of a sinusoidal curve. Find detailed examples and additional practice questions below to help reinforce your understanding and build confidence in graphing these functions. Let’s get started!
What is a sinusoidal function?
A sinusoidal function is a periodic function that can be described by either a sine or cosine equation. The standard equation of a sinusoidal function takes one of the following forms:
$$y = A\sin(B(x - C)) + D \quad \text{or} \quad y = A\cos(B(x - C)) + D$$
In any case, the values of $A$, $B$, $C$, and $D$ represent different aspects of the graph. As an example, consider the graph of the function $y = 2\sin\left(\frac{1}{2} \left(x - \frac{\pi}{2} \right)\right) + 1$ below.
$A$ represents the amplitude, which is equal to the absolute value of $A$ $\left(|A|\right)$. The amplitude is the distance from the midline of the graph to any maximum or minimum value. It is always positive, thus the absolute value. A negative value of $A$ indicates a reflection over the midline.
Amplitude: $2$
$B$ represents the period, which is equal to $\frac{2\pi}{B}$. The period is the horizontal distance of a full cycle. It is more easily calculated by finding the distance between two consecutive maximums (or minimums). Alternatively, measure the distance along the midline from where a cycle begins to where it ends.
Period: $4\pi$
$C$ represents the phase shift. A positive value of $C$ indicates a horizontal shift to the left, while a negative value of $C$ indicates a horizontal shift to the right. In many cases, the equation must be manipulated to identify the phase shift. Consider, for example, the function $y = 2\sin\left(\frac{1}{2}x - \frac{\pi}{4}\right) + 1$. In this case, $-\frac{\pi}{4}$ does not indicate a horizontal shift $\frac{\pi}{4}$ units to the rights. Instead, notice this is the same equation graphed before, where $B$ has been distributed to eliminate the second parentheses. To find the correct value of $C$, simply factor $B$ out, turning $\frac{1}{2}x-\frac{\pi}{4}$ into $\frac{1}{2}\left(x-\frac{\pi}{2}\right)$.
Phase shift: right $\frac{\pi}{2}$
Lastly, $D$ represents the vertical shift. A positive value of $D$ indicates a shift up, while a negative value of $D$ indicates a shift down. The midline is represented by the equation $y=D$.
Vertical shift: up $1$ (midline $y=1$)
Graphing a sinusoidal function step by step.
- The first step to graph a sinusoidal function is identifying the amplitude, period, phase shift, and vertical shift.
- Begin by sketching the midline at $y=D$. The graph oscillates around this line.
- Use the amplitude to sketch the limits of the function. A sinusoidal function reaches its maximums at $D+|A|$, and its minimums at $D-|A|$.
- Identify the starting point. Before considering phase shift or reflection, sine functions begin at the midline, then head up to a maximum. Cosine functions, on the other hand, begin at a maximum. Consider any reflection, given by a negative value of $A$, and the phase shift to identify the starting point. If the graph has not been reflected, a starting point for a sine function is $\left(-C,D\right)$. For a cosine function is $\left(-C,D+|A|\right)$. If the graph has been reflected, the starting point for a sine function is still $\left(-C,D\right)$, but it will then head down to a minimum. A reflected cosine function begins at a minimum, $\left(-C,D-|A|\right)$.
- Consider the period to identify additional points. The function will be back on the same level (midline, maximum, or minimum) as the starting point after the length of a period. For example, if the starting point is $\left(\frac{\pi}{2},1\right)$, and the period is $4\pi$, that cycle ends at $\left(\frac{\pi}{2}+4\pi,1\right)$ or $\left(\frac{9\pi}{2},1\right)$. The remaining points of interest between the starting point and the end point of the cycle -which include maximums, minimums, or points on the midline- are all equally spaced. So, use the period to identify their exact coordinates. After that, the cycles will repeat again to create the graph of the function.
Examples
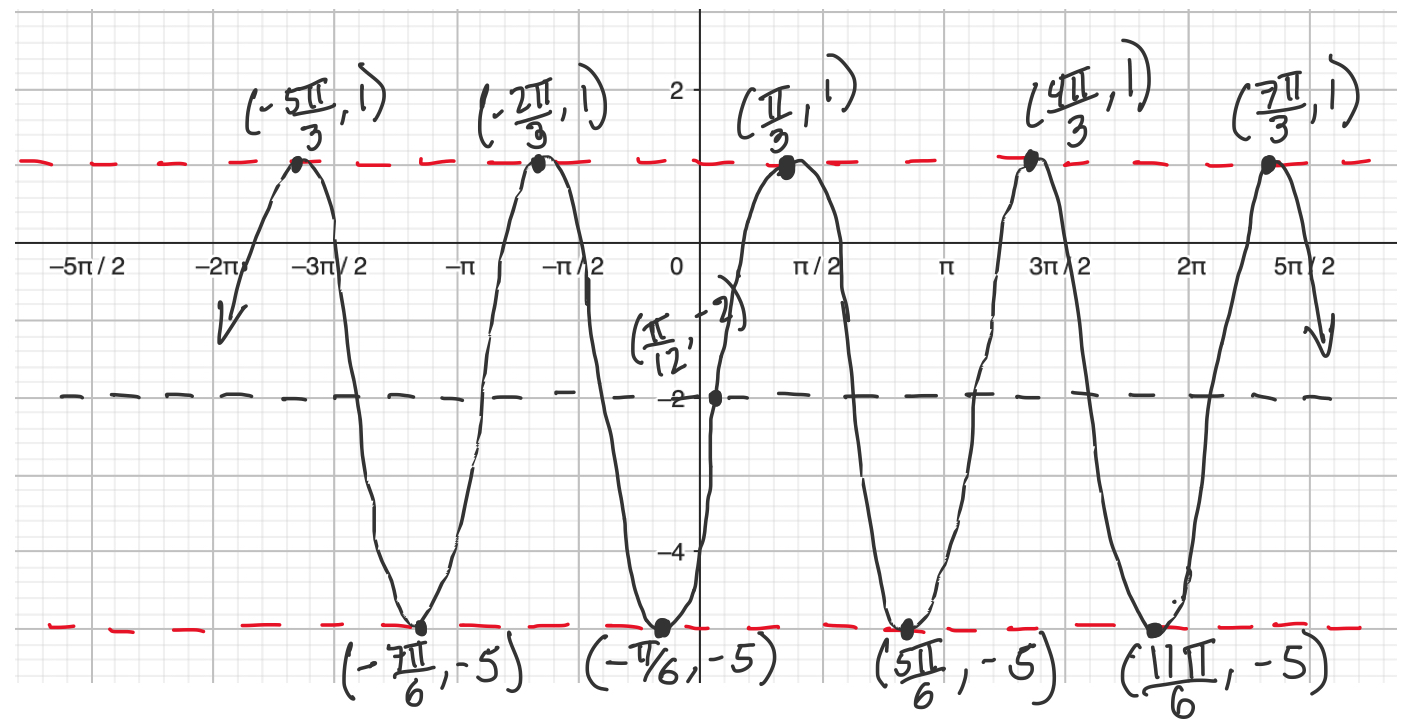
Example 1. Graph the sinusoidal function below.
$$y = -3\cos\left(2x + \frac{\pi}{3}\right) - 2$$
Amplitude: $3$ (reflected over midline)
Period: $\frac{2\pi}{2}=\pi$
Phase shift: $2x+\frac{\pi}{3}=2\left(x+\frac{\pi}{6}\right)$, left $\frac{\pi}{6}$
Vertical shift: down $2$ (midline $y=-2$)
Since the cosine function was shifted left $\frac{\pi}{6}$, down $2$, and reflected, a starting point could be the minimum $\left(-\frac{\pi}{6},-5\right)$. The graph will reach a minimum again at $\left(-\frac{\pi}{6}+\pi,-5\right)$. A maximum will be located in between these two minimums at $\left(\frac{\pi}{3},1\right)$.
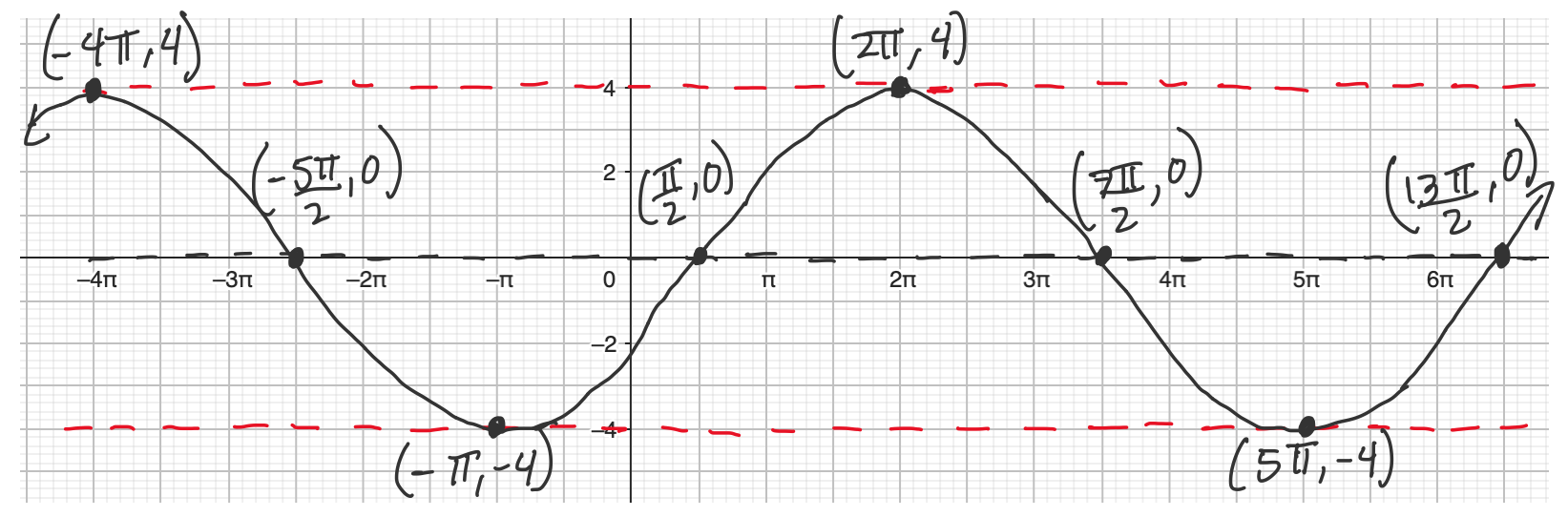
Example 2. Graph the sinusoidal function below.
$$y=4\sin\left(\frac{1}{3}x-\frac{\pi}{6}\right)$$
Amplitude: $4$
Period: $\frac{2\pi}{\frac{1}{3}}=6\pi$
Phase shift: $\frac{1}{3}x-\frac{\pi}{6}=\frac{1}{3}\left(x-\frac{\pi}{2}\right)$, right $\frac{\pi}{2}$
Vertical shift: none (midline $y=0$)
Since the sine function was shifted right $\frac{\pi}{2}$, a starting point could be $\left(\frac{\pi}{2},0\right)$. The graph will intersect the midline again at $\left(\frac{\pi}{2}+3\pi,0\right)$, and again at $\left(\frac{\pi}{2}+6\pi,0\right)$. It will have a maximum in between the first two points intersecting the midline, at $\left(2\pi,4\right)$. And a minimum in between the second pair of points intersecting the midline, at $\left(5\pi,-4\right)$.
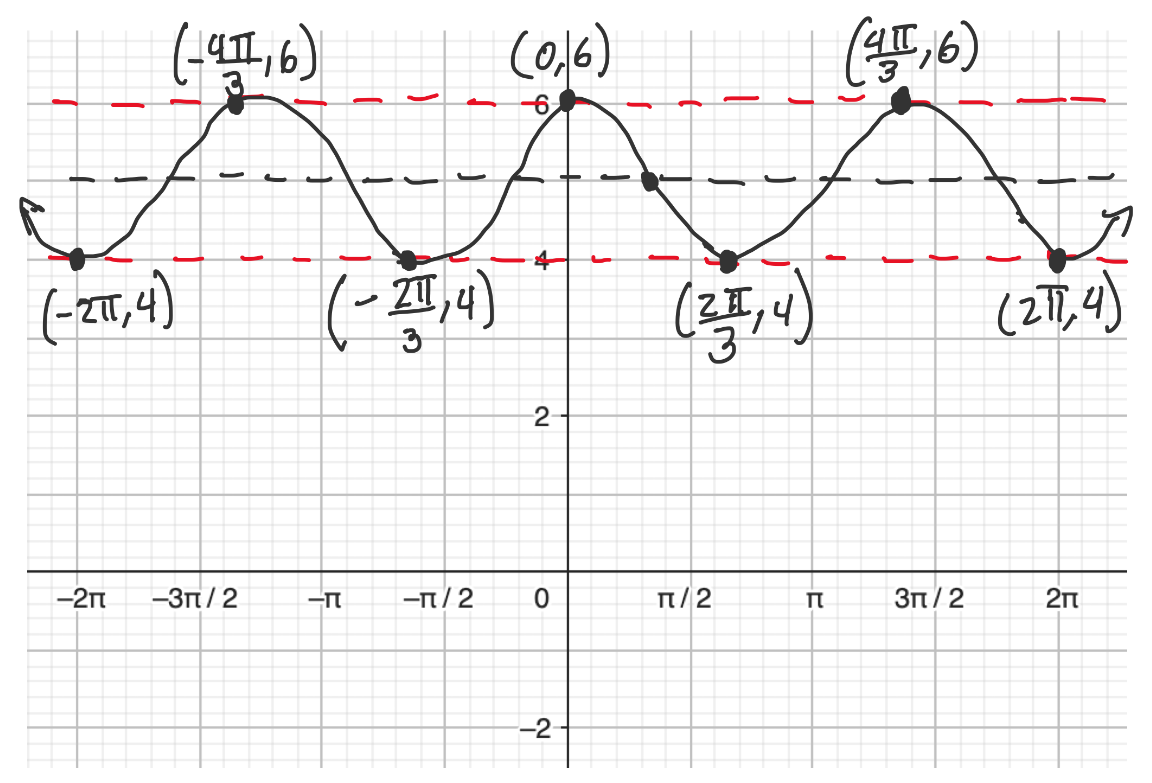
Example 3. Graph the sinusoidal function below.
$$y = \cos\left(\frac{3}{2} x\right) + 5$$
Amplitude: $1$
Period: $\frac{2\pi}{\frac{3}{2}} = \frac{4\pi}{3}$
Phase shift: none
Vertical shift: up $5$ (midline $y = 5$)
Since the cosine function was shifted up, a starting point could be the maximum $\left(0,6\right)$. The graph will reach another maximum at $\left(\frac{4\pi}{3},6\right)$. A minimum will be located in between these two maximums at $\left(\frac{2\pi}{3},4\right)$.
Example 4. Graph the sinusoidal function below.
$$y = -\frac{1}{2} \sin\left(\frac{2\pi}{3} x\right)$$
Amplitude: $\frac{1}{2}$ (reflected over the x-axis)
Period: $\frac{2\pi}{\frac{2\pi}{3}}=3$
Phase shift: none
Vertical shift: none (midline $y=0$)
Since the sine function has been reflected, a starting point could be $\left(0,0\right)$. The graph will intersect the midline again at $\left(\frac{3}{2},0\right)$, and again at $\left(3,0\right)$. It will have a minimum between the first two points intersecting the midline at $\left(\frac{3}{4},-\frac{1}{2}\right)$. And a maximum between the second pair of points intersecting the midline at $\left(\frac{9}{4},\frac{1}{2}\right)$.
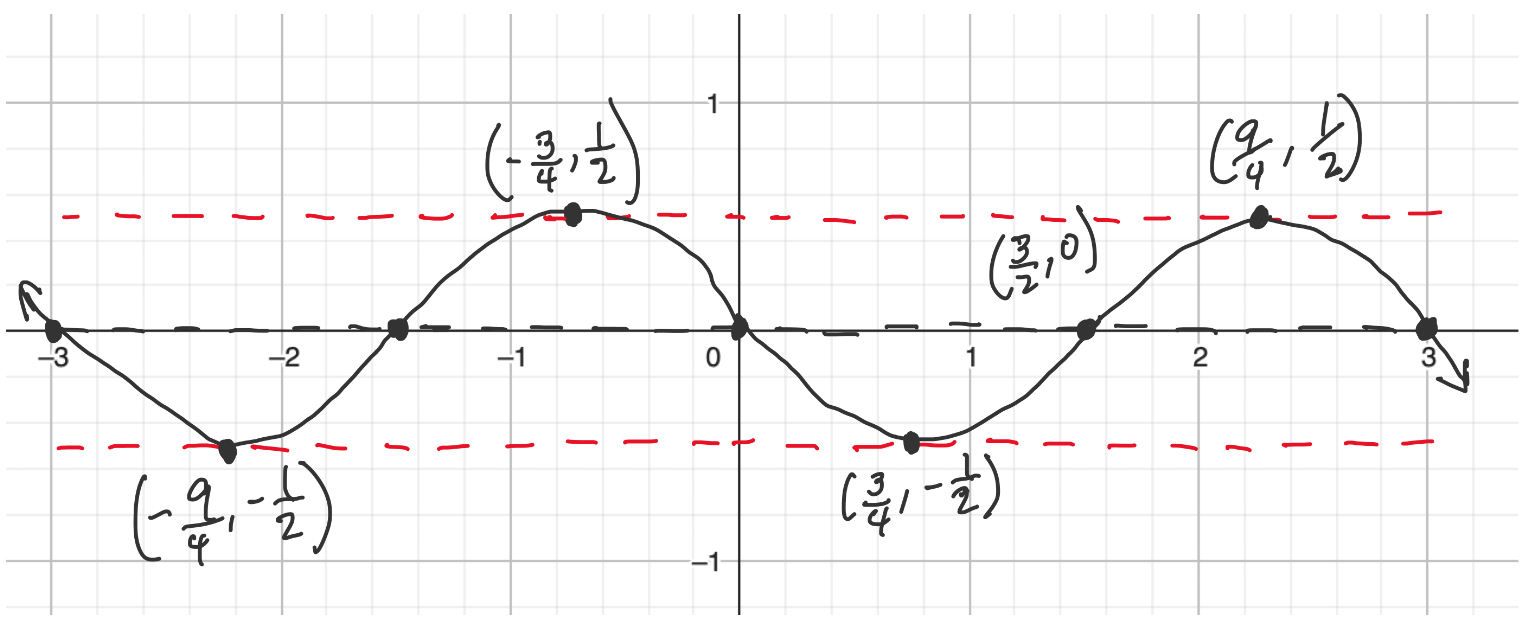
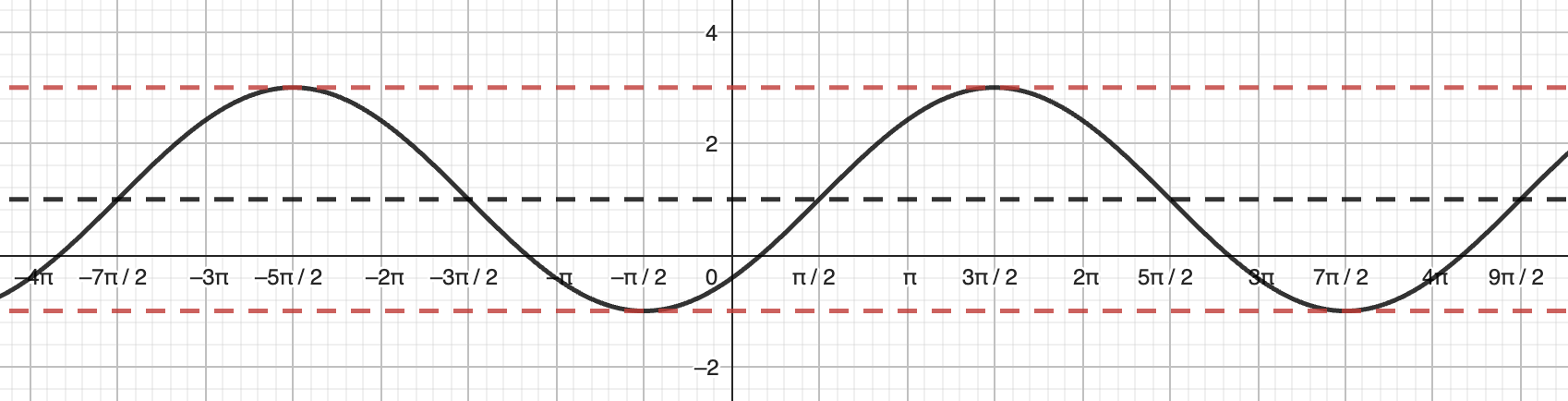
For examples 5-8 use the graph below.
Example 5. Find an equation for the graph above using sine function and a positive A value.
The amplitude, period, and vertical shift can be identified directly from the graph.
Amplitude: $3$, so $A=3$
Period: $\frac{2\pi}{B}=\pi$, so $B=2$
Vertical shift: up $1$, so $D=1$
The phase shift can be identified after selecting a starting point that satisfies the given conditions. For a sine function with no reflection (positive A value), the starting point lies on the midline, then reaches up to a maximum. A starting point for this function could be $\left(\frac{\pi}{4},1\right)$. Notice that this is not the only option. For example, $\left(-\frac{3\pi}{4},1\right)$ is another point that satisfies the given conditions, so is $\left(\frac{5\pi}{4},1\right)$ and infinitely many other points.
Phase shift: right $\frac{\pi}{4}$, so $C=-\frac{\pi}{4}$
Now we can write the equation as $y=3\sin\left(2\left(x-\frac{\pi}{4}\right)\right)+1$ or $y=3\sin\left(2x-\frac{\pi}{2}\right)+1$.
Example 6. Find an equation for the graph above using a cosine function and a negative A value.
Amplitude: $3$, so $A=-3$
Period: $\frac{2\pi}{B}=\pi$, so $B=2$
Vertical shift: up $1$, so $D=1$
For a cosine function that has been reflected (negative $A$ value), the starting point must be a minimum, such as $\left(0,-2\right)$.
Phase shift: none, so $C=0$
An equation that satisfies the given conditions is $y=-3\cos\left(2x\right)+1$.
Example 7. Find an equation for the graph above using sine function and a negative A value.
Amplitude: $3$, so $A=-3$
Period: $\frac{2\pi}{B}=\pi$, so $B=2$
Vertical shift: up $1$, so $D=1$
For a sine function that has been reflected (negative $A$ value), the starting point lies on the midline, then reaches down to a minimum. A starting point for this function could be $\left(-\frac{\pi}{4},1\right)$.
Phase shift: left $\frac{\pi}{4}$, so $C=\frac{\pi}{4}$
An equation that satisfies the given conditions is $y=-3\sin(2(x+\frac{\pi}{4}))+1$ or $y=-3\sin(2x+\frac{\pi}{2}))+1$
Example 8. Find an equation for the graph above using cosine function and a positive A value.
Amplitude: $3$, so $A=3$
Period: $\frac{2\pi}{B}=\pi$, so $B=2$
Vertical shift: up $1$, so $D=1$
For a cosine function with no reflection (positive $A$ value), the starting point must be a maximum, such as $\left(\frac{\pi}{2},4\right)$.
Phase shift: right $\frac{\pi}{2}$, so $C=-\frac{\pi}{2}$
An equation that satisfies the given conditions is $y=3\cos\left(2\left(x-\frac{\pi}{2}\right)\right)+1$ or $y=3\cos\left(2x-\pi\right)+1$.
Practice Questions
-
Consider the equation $y=3\sin\left(2x-\pi\right)+4$. Identify the amplitude, period, phase shift, vertical shift, and graph the function.
-
Write the equation of a cosine function with amplitude $2$, period $4\pi$, phase shift of $\frac{\pi}{2}$ to the right, and vertical shift of $3$ down.
-
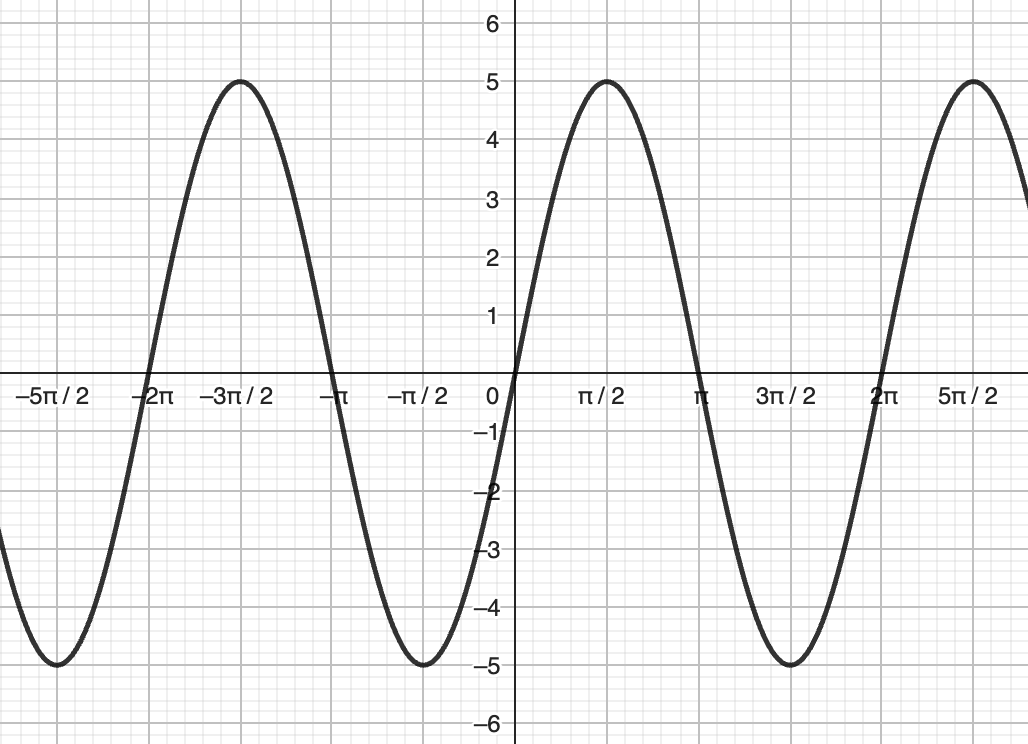
A graph is shown with a sinusoidal curve passing through the origin, reaching a maximum of $5$ at $x=\frac{\pi}{2}$, and a minimum of $-5$ at $x=\frac{3\pi}{2}$. Write an equation for the function in terms of sine, and another in terms of cosine.
-
For each equation below, describe the transformations from the basic sine or cosine function.
$$y=-4\sin\left(x-\frac{\pi}{4}\right)+2$$
$$y=2\cos\left(3x\right)-1$$
$$y=\sin\left(\frac{1}{2}x+\frac{\pi}{6}\right)$$
$$y=-\cos\left(2x\right)+3$$
- A Ferris wheel follows a sinusoidal motion. At its lowest point, the rider is $2$ meters above the ground, and at its highest point, the rider is $42$ meters above the ground. The wheel takes $10$ seconds to complete one full rotation. Assuming the rider starts at the lowest point at $t=0$, write a sine equation to model the rider’s height over time.
Answer Key
-
Amplitude: $3$
Period: $\pi$
Phase shift: right $\frac{\pi}{2}$
Vertical shift: up $4$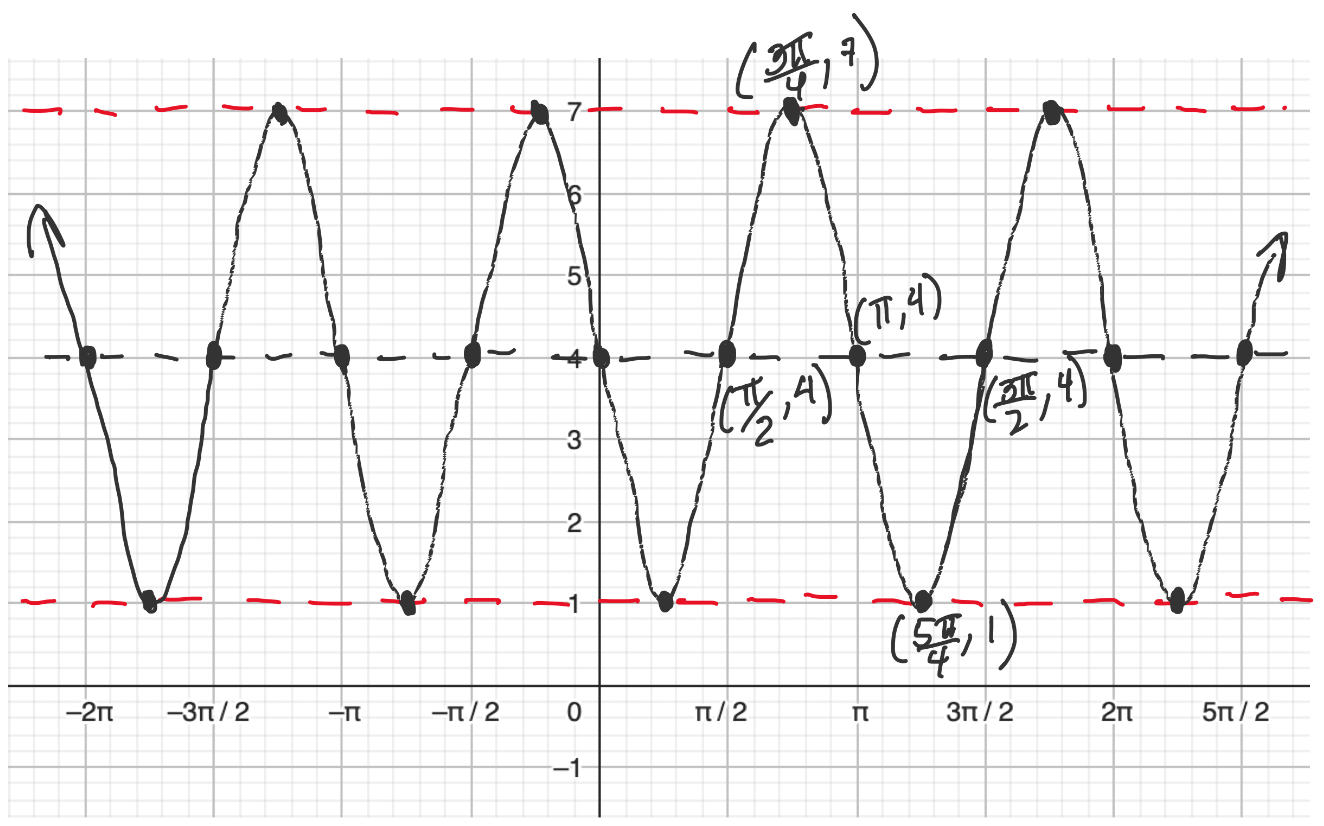
-
$y=2\cos\left(\frac{1}{2}x-\frac{\pi}{4}\right)-3$
-
$y=5\sin\left(x\right)$
$y=5\cos\left(x-\frac{\pi}{2}\right)$ -
-
$y=-4\sin\left(x-\frac{\pi}{4}\right)+2$
The sine functions was shifted right $\frac{\pi}{4}$, up $2$, vertically stretched by a factor of $4$, and reflected over the line $y=2$. -
$y=2\cos\left(3x\right)-1$
The cosine function was shifted down $1$, vertically stretched by a factor of 2, and horizontally compressed to new period $\frac{2\pi}{3}$. -
$y=\sin\left(\frac{1}{2}x+\frac{\pi}{6}\right)$
The sine function was shifted left $\frac{\pi}{3}$, and horizontally streched to new period $4\pi$. -
$y=-\cos\left(2x\right)+3$
The cosine function was shifted up 3, horizontally compressed to new period $\pi$, and reflected over the line $y=3$.
-
- $y=20\sin\left(\frac{\pi}{5}t-\frac{\pi}{2}\right)+22$